Ako nájsť dĺžku tretej strany trojuholníka?

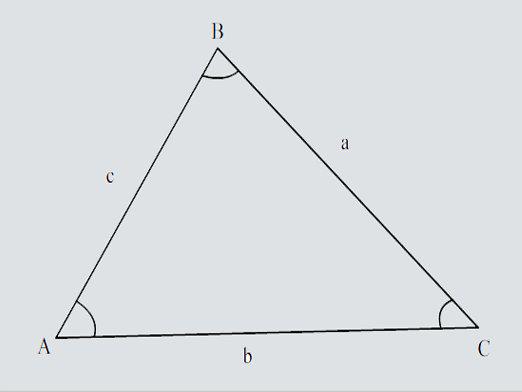
Problém riešenia trojuholníkov (toto je názov takýchto problémov) je riešený špeciálnou časťou geometrie - trigonometria.

Dĺžka oboch strán trojuholníka

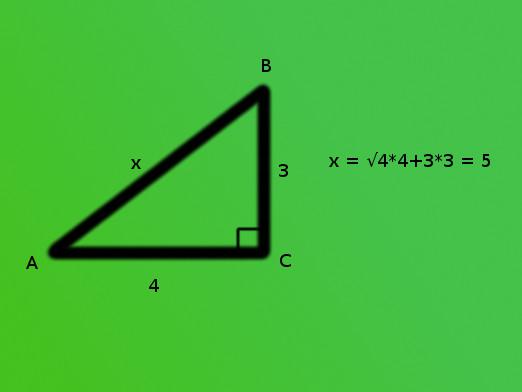
Nájdite dĺžku tretej strany trojuholníkaobdĺžnikový naznačil, že starý matematik Pythagoras je známy každému. Základom je obdĺžnikový trojuholník, teda ten, v ktorom je jeden z uhlov rovný 90 stupňom. Priľahlé strany tohto rohu sú vždy označované ako nohy, tretia, najväčšia strana, sa nazýva "hypotenuse". Pythagorovu vetu je nasledovné: "štvorec dĺžky hypotenze sa rovná súčtu štvorcov dĺžok nohy."

Ak chcete vyriešiť takýto problém, hodnotu dĺžky jednéhoOznačíme nohu ako X (X) a druhú Y (jarmo), dĺžka hypotenuse môže byť označená ako Z (z). Teraz napíšeme vzorec na výpočet dĺžky hypotézy: Z je štvorcový = X je štvorcový + Y je štvorcový. Vychádzajúc z takéhoto vzorca, získame konečne hodnotu štvorca dĺžky hypotenze. Preto na získanie hodnoty dĺžky hypotenze je stále potrebné extrahovať druhú odmocninu výslednej sumy dĺžok nohy.

Predtým sme považovali za ideálnu voľbu, kedyje potrebné určiť dĺžku hypotenze. Ak v probléme nie je známa dĺžka jednej nohy, potom môžeme na základe vyššie uvedenej vety odvodiť odvodený vzorec. Štvorec dĺžky jednej nohy sa rovná hodnote získanej odčítaním štvorca dĺžky druhej nohy od štvorca dĺžky hypotenze: X je štvorcový = Z je štvorcový - Y je štvorcový. Posledným krokom je nevyhnutne extrakcia druhej odmocniny získanej hodnoty.

Napríklad, vezmite jednoduché hodnoty dĺžkykyvety: 2 a 3 centimetre. Jednoduchými matematickými operáciami dostaneme štvorcový Z = 4 + 9 = 13. To znamená, že Z je približne 3,6 centimetra. Ak vylúčime zarovnanie hodnôt, ukazuje sa, že Z = 2 + 3 = 5 centimetrov, čo nezodpovedá pravde.

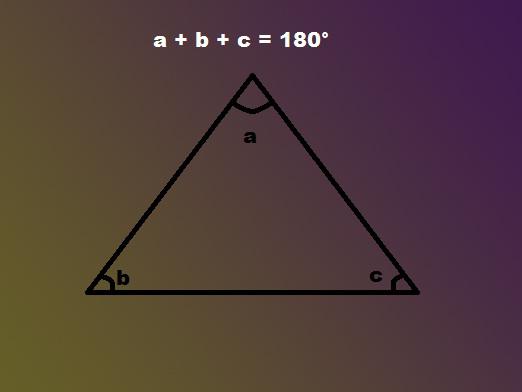
Dĺžkou oboch strán a hodnotou uhla medzi nimi

Je možné nájsť dĺžku tretej strany trojuholníka,pomocou kosínovej vety. Táto geometrická veta je nasledujúce: štvorec jedna strana trojuholníka je rovná hodnote získanej odpočítaním dvojnásobok dĺžky strán produkt známy a kosínus uhla, ktorý je umiestnený medzi nimi, zo súčtu štvorcov známej dĺžky strán.

V matematickej podobe vyzerá takýto vzorectakto: Z je štvorcový = X2 + Y2-2 * X * Y * cosC. Tu X, Y, Z označujú dĺžku všetkých strán trojuholníka a C je hodnota v stupňoch uhla, ktorý sa nachádza medzi známymi stranami.

Napríklad používame trojuholník, ktorý je známyktorých strany sa rovnajú 2 a 4 centimetre a uhol medzi nimi je 60 stupňov. Využívame vyššie uvedený vzorec a dostávame: Z štvorcový = 4 + 16-2 * 2 * 4 * cos60 = 20-8 = 12. Dĺžka neznámej strany je 3,46 cm.