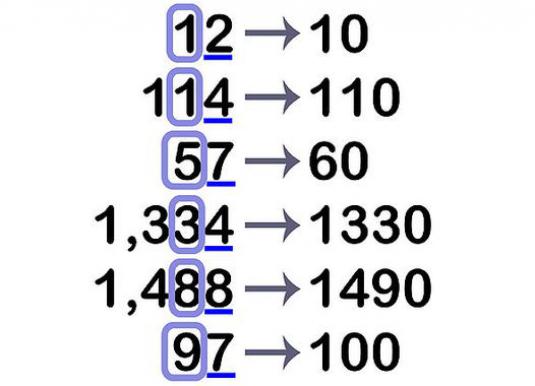
Pravidlá zaokrúhľovania

V niektorých prípadoch presný počet v divíziinie je možné v zásade určiť určitú sumu pre konkrétne číslo. Napríklad pri rozdelení 10 na 3, dostaneme 3,33333333333 ... .3, to znamená, že toto číslo nemožno použiť na počítanie konkrétnych položiek v iných situáciách. Toto číslo by sa malo uviesť na určitú číslicu, napríklad na celé číslo alebo na číslo s desatinnou čiarkou. Ak dáme 3,33333333333 ... .3 na celé číslo, dostanete 3 a dávať 3,33333333333 ... .3 číslu s desatinným miestom, dostaneme 3,3.

Pravidlá zaokrúhľovania

Čo je zaokrúhľovanie? Toto je odmietnutie niekoľkých číslic, ktoré sú posledné zo série presných čísel. Takže po našom príklade sme klesli všetky najnovších údajov získať celé číslo (3) a zahodené číslice, odchádzajúci jediný desiatkovú číslicu (3,3). Číslo môže byť zaokrúhlené na stotiny a tisíce, desať tisíc a ďalšie čísla. Všetko závisí od toho, koľko potrebujete získať presné číslo. Napríklad, pri výrobe liekov, množstvo každej zložky lieku sa užíva s najvyššou presnosťou, pretože tisícinu gramu môže byť dokonca smrteľné. Ak je potrebné vypočítať, aký je pokrok študentov v škole, najčastejšie sa používa číslo s desatinnou alebo stotinkou.

Pozrime sa na ďalší príkladpravidlá zaokrúhľovania. Napríklad, tam je celý rad 3.583333, ktorá musí byť zaokrúhlená na tisíciny - po zaokrúhlení, s bodom by sme mali zostať tri číslice, to znamená, že výsledok bude číslo 3583. Ak sa toto číslo zaokrúhľuje na desatiny, nedostaneme 3,5, ale 3,6, pretože po "5" je číslo "8", ktoré je pri zaokrúhľovaní už priradené k "10". Tak, podľa pravidiel zaokrúhľovania, je potrebné vedieť, či sú čísla vyššie ako "5", bude posledný číslica chcete ušetriť, sa zvýši o 1. V prípade výskytu čísel, menej ako "5", druhé udržal postava zostáva nezmenený. Takéto pravidlá zaokrúhľovania platia bez ohľadu na celé číslo alebo až desiatky, stotiny atď. je potrebné zaokrúhliť číslo.

Vo väčšine prípadov, ak je to potrebnézaokrúhľovanie čísla, v ktorom je posledná číslica "5", tento proces nie je správne vykonaný. Existuje však aj pravidlo zaokrúhľovania, ktoré sa zaoberá práve takými prípadmi. Zoberme si príklad. Je potrebné zaokrúhliť číslo 3.25 na desatinu. Použitím pravidiel zaokrúhlenia získame výsledok 3.2. To znamená, že ak nie je žiadna číslica po "päť" alebo nula, potom posledná číslica zostane nezmenená, ale iba ak je rovnomerná - v našom prípade "2" je sudé číslo. Ak by sme mali zaokrúhľovať 3,35, výsledkom by bolo číslo 3.4. Pretože v súlade s pravidlami zaokrúhľovania, za prítomnosti nepárneho čísla pred "5", ktorý musí byť odstránený, nepárne číslo sa zvyšuje o 1. Ale iba za podmienky, že po "5" nie sú žiadne významné čísla. V mnohých prípadoch možno použiť zjednodušené pravidlá, podľa ktorých, ak sú číslice od 0 do 4 pre poslednú uloženú číslicu, uložená číslica sa nemení. Ak existujú iné číslice, posledná číslica sa zvýši o 1.