Ako vyriešiť pomer?

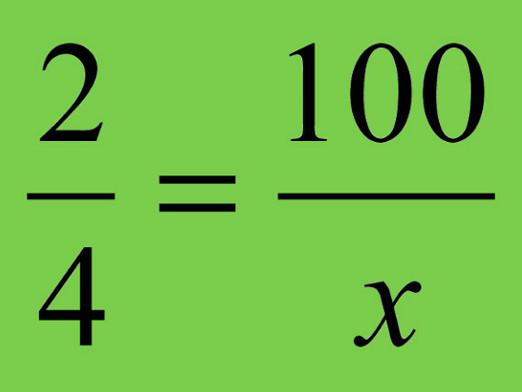
Všetci kedysi učili v hodinách matematických rozmerov. Ako vyriešiť podiel, náš článok povie.

Zvážte definíciu pomeru. Predpokladajme, že máme štyri nenulové čísla A, B, B a F. Sú také, že A: D je B: F. Táto rovnosť sa nazýva pomer. Proporcionalita je rovnosť takýchto dvoch vzťahov. V takomto pomere sú čísla A a T extrémne pomery a čísla D a B sú priemerné pomery.

Prečítajte si tento pomer takto: "A odkazuje na B ako B označuje G".

Použitím vlastností bežných frakcií máme tvrdenia, ktoré nám pomôžu pri riešení rozmerov:

Pomer A: B sa rovná B: F môže byť napísané týmto spôsobom: A: B sa rovná B: D.
Extrémne členovia tohto podielu sa môžu zameniť. To znamená, že ak A: D je B: T, potom T: D je B: A.
Priemerní členovia daného podielu môžu byť tiež vymenení. To znamená, že ak A: D je B: T, potom A: B sa rovná B: T.
Produkt extrémnych podmienok tohto podielu jeprodukt priemerných členov. To znamená, že ak A: D je B: T, potom AH sa rovná BV - to je hlavná vlastnosť takéhoto podielu. Existujú aj iné základné vlastnosti pomeru:
- Zrušenie pomeru. To znamená, že ak A: D je B: T, potom B: A sa rovná T: B.
- Násobenie členov tohto podielu je krížové. To znamená, že ak A: D je B: T, potom A · F sa rovná B · B.
- Preskupenie extrémnych a stredných členov podielu. To znamená, že keď A: D je B: T, potom:
- A: B sa rovná B: D je permutácia priemerných pomerov.
- D: D je B: A je permutácia extrémnych pomerov.
- Zostavenie pomeru odčítaním a pridaním. To znamená, keď A: D je B: T, potom
- (A-B): (Б-Г) sa rovná A: B sa rovná B: Г - kompilácia odčítaním.
- (A + B): (B + T) sa rovná A: D je B: T je kompozícia pridaním.
- Zníženie a zvýšenie. To znamená, že keď A: D je B: T, potom:
- (A-B): D sa rovná (B-D): D je pokles pomeru.
- (A + B): D sa rovná (B + F): T je nárast podielu.