Čo je to lichobežník?

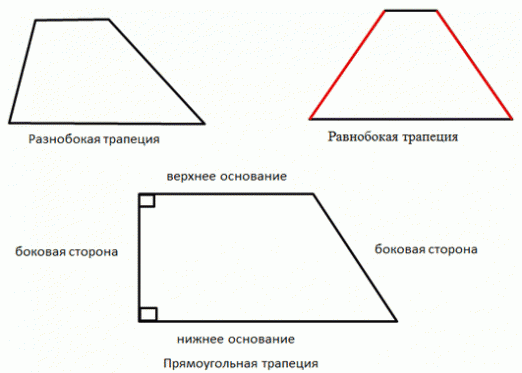
Každý, kto študoval v škole, v triedegeometria, študoval to, čo lichobežník. Toto slovo sa používalo aj v starovekom Grécku av tomto jazyku znamenalo "stôl, stôl alebo jedlo". Slovo "lichobežník" je štvorčlenná postava, v ktorej sú obe strany paralelné, ostatné dve strany nie sú paralelné súčasne.

Trapézové vlastnosti

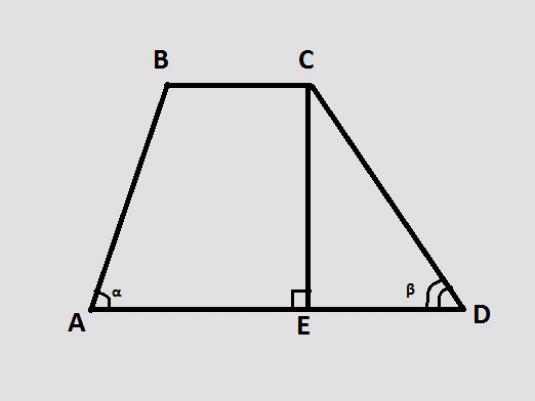
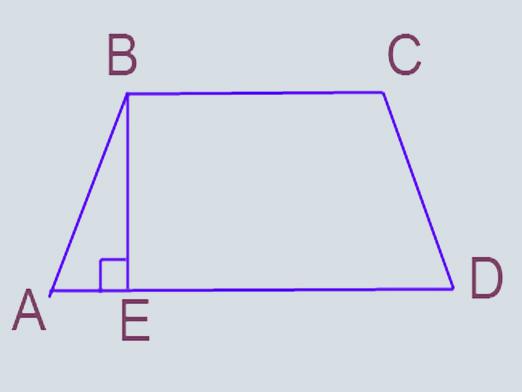
Paralelné strany lichobežníka sú považované za základčísla a ostatné strany sú bočné. Trapéz má stredovú čiaru, ktorá spája boky uprostred. Aj na tomto obrázku môžete nakresliť kolmúru z jedného bodu na spodku do druhého na druhom základe, potom sa táto kolmica nazýva výška.

Existujú také lichobežníky:

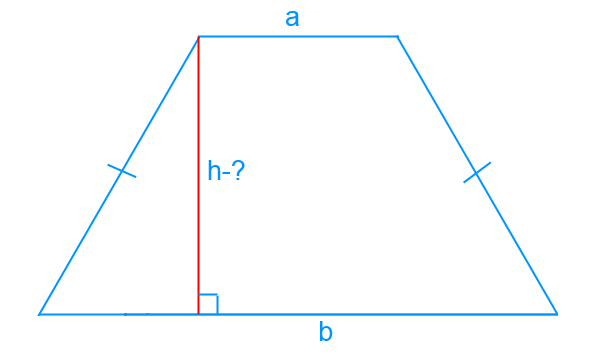
isosceles - keď sú strany rovnaké;
pravouhlý - keď sú strany rohov 90 stupňov.

Riadok takejto postavičky, ktorá sa nachádza v strede,je rovnobežná so základňou, číselne sa rovná polovici súčtu dvoch základov. Ďalšia vlastnosť sa týka uhlov lichobežníka, teda súčet týchto uhlov je 180 stupňov.

V rovnobežnom lichobežníku sú základné uhly párové,napríklad uhol A = D a uhol B = C. Rovnako v rovnobežnom lichobežníku sú diagonály, ktoré spájajú opačné body, rovnaké, získame AC = BD.

Ak je súčet dvoch hlavných strán obrázku úplnýje totožná so súčtom bočných strán, potom môže byť do takéhoto obrázku zapísaná kružnica. Navyše sú trojuholníky, ktoré ležia na stranách lichobežníka, rovnaké.

Segment, ktorý leží pozdĺž strednej čiary aspája stred diagonálov, sa rovná polovici rozdielu strán bázy. Na jednej línii leží bod, v ktorom sa bočné strany pretínajú a bod, v ktorom sa spoja diagonály lichobežníka.

rozloha

Ak chcete zistiť oblasť lichobežníka, musíte postupovať takto:

S = (a + b) / 2 h

V ňom: "a" a "in" - pozemky, "h" - výška postavy.

Ak dĺžky lichobežníc nie sú známe aiba výška a stredná čiara, v tomto prípade platí nasledujúci vzorec: S = m * h. Ak je hodnota "m" dĺžka stredovej čiary. Tieto dve vzorce sú ekvivalentné a môžeme povedať, že priemerná čiara je m = (a + b) / 2.

Ak chcete poznať oblasť lichobežníkového lichobežníka,potrebujete poznať hodnotu uhla. Tu je vzorec: S = (a - c * cos y) c * sin y = (b - c * cos y) c * sin y. Kde a je dlhé a b je krátke, c je strana a y je uhol medzi dlhou základňou a bočnou stranou.

Pozrite si aj naše ďalšie články na tejto stránke: