Čo je to rovnobežnosť?

V geometrii sú kľúčové pojmyrovina, bod, čiara a uhol. Pomocou týchto výrazov môžete opísať ľubovoľné geometrické číslo. Polyhedra sú zvyčajne opísané pomocou jednoduchších tvarov, ktoré ležia v jednej rovine, ako je kruh, trojuholník, štvorec, obdĺžnik atď. V tomto článku sa budeme diskutovať o tom, čo sa okno, popisovať jednotlivé druhy hranolov, jej vlastnosti, aké prvky, ktoré zahŕňa, a tiež dať základné vzorce pre výpočet plochy a objemu boxu pre každý druh.

definícia

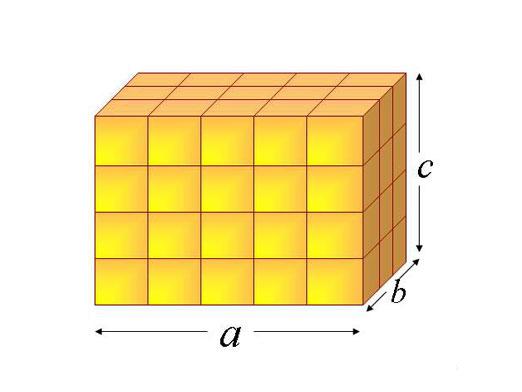
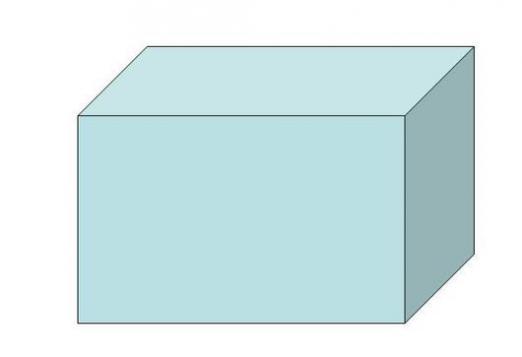
Paralelipiped v trojrozmernom priestore je hranol, ktorého všetky strany sú paralelogrammi. Preto môže mať len tri páry paralelných paralelogramov alebo šesť tvárí.

Ak chcete zobraziť krabicu, predstavte si topredstavte si štandardnú tehlu. Tehla je dobrým príkladom obdĺžnikového rovnobežnostenca, ktorý si dieťa dokáže predstaviť. Ďalšie príklady môžu slúžiť ako viacpodlažné panelové domy, skrine, kontajnery na skladovanie potravinárskych výrobkov vhodného tvaru atď.

Druh obrázku

Existujú iba dva typy rovnobežníc:

Obdĺžnikové, ktorých všetky bočné plochy sú v uhle 90 °^o k základni a sú obdĺžniky.
Šikmé bočné plochy, ktoré sú umiestnené pod určitým uhlom k základni.

Aké prvky možno rozdeliť do tohto tvaru?

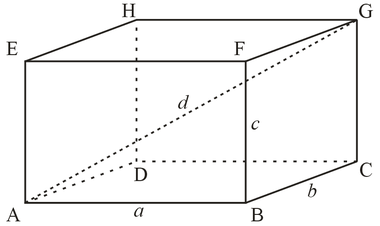
Rovnako ako v každom inom geometrickom obrázku, vsú rovnobežne lepené akékoľvek dve plochy so spoločným okrajom, ktoré sa nazývajú priľahlé a tie, ktoré ich nemajú, sú paralelné (začínajúc vlastnosťou paralelogramu, ktorý má párové paralelné protiľahlé strany).
Vrcholy rovnobežnosti, ktoré nie sú na jednej strane, sa nazývajú opačne.
Segment spájajúci takéto vrcholy je diagonál.
Dĺžky troch okrajov obdĺžnikového rovnobežnostenia spájajúceho na jednom vrchole sú jeho rozmery (menovite jeho dĺžka, šírka a výška).

Vlastnosti tvaru

Vždy je postavená symetricky vzhľadom na stred diagonály.
Priesečník všetkých uhlopriečok rozdeľuje každú uhlopriečku na dva rovnaké segmenty.
Opačné plochy majú rovnakú dĺžku a ležia na rovnobežných priamkach.
Ak kombinujete štvorce všetkých rozmerov krabice, výsledná hodnota sa bude rovnať štvorcu dĺžky diagonály.

Výpočtové vzorce

Vzorce pre každý konkrétny prípad rovnobežnosti budú mať svoje vlastné.

Pre ľubovoľný rovnobežnosť je pravdatvrdenie, že jeho objem sa rovná absolútnej hodnote trojitého skalárneho produktu vektorov troch strán vychádzajúcich z jedného vrcholu. Neexistuje však žiadny vzorec na výpočet objemu ľubovoľného rovnobežnostenca.

Pri obdĺžnikovom rovnobežku sa uplatňujú tieto vzorce:

V = a * b * c;
Sb = 2 x c * (a + b);
Sn = 2 * (a * b + b * c + a * c).

kde:

V je objem čísla;
Sb je oblasť bočného povrchu;
Sn je celková plocha povrchu;
a je dĺžka;
b je šírka;
c - výška.

Ďalší konkrétny prípad rovnobežnosti, vktorého všetky strany sú štvorce, je kocka. Ak je jedna či druhá strana štvorca označená písmenom a, potom pre plochu povrchu a objem daného obrázku je možné použiť tieto vzorce:

S = 6 * a * 2;
V = 3 * a.

kde:

S je oblasť postavy,
V je objem čísla,
a je dĺžka tváre postavy.

Posledná odroda, ktorú zvažujemerovnobežnosť je rovná rovnobežnosť. Aký je rozdiel medzi priamym rovnobežnostencom a obdĺžnikovým rovnobežnostencom, opýtajte sa. Faktom je, že základom obdĺžnikového rovnobežnostenca môže byť akýkoľvek rovnobežník a základ rovného rovnobežnostenca je len obdĺžnik. Ak označíme obvod základne, ktorý sa rovná súčtu dĺžok všetkých strán, napríklad Po, a výška je označená písmenom h, máme právo na výpočet objemu a plôch celkových a bočných plôch nasledovné vzorce: