Ako nájsť oblasť rovnobežnosteny?

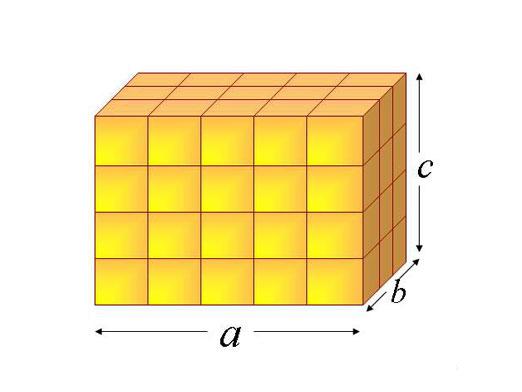
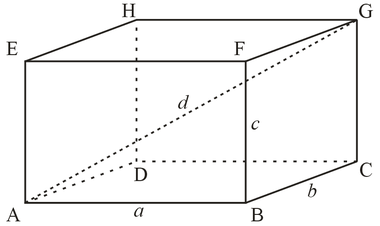
V geometrickom obrázku má rovnobežnosťšesť tvárí - štyri základné a dve základne (podľa definície sú to všetky paralelogramy). Ak sú všetky šesť obdĺžnikov, rovnobežnosť bude rovná. Okraje na protiľahlých stranách sú rovnaké a sú paralelné. Štyri diagonály rovnobežnosti sa zbiehajú v jednom bode a rozdeľujú sa na dve.

Ak chcete zistiť, ako nájsť oblasťje potrebné najskôr vypočítať plochu všetkých jej základov (označenú písmenom -a), jej bočnou stranou (označenou písmenom -b), pričom sa určuje dĺžka základne a okraja.

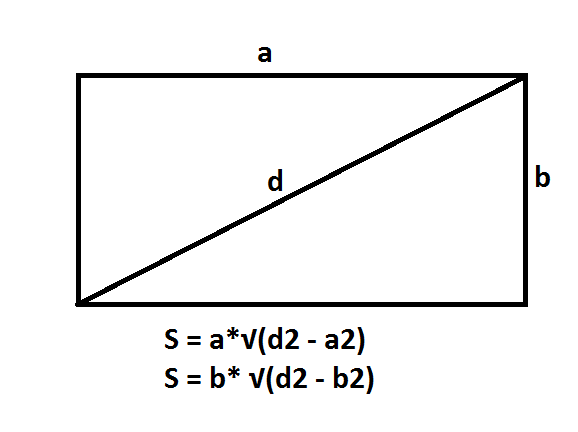
Najskôr nakreslíme výšku paralelogramu (označenú písmenom - h), potom okraj rovnobežnostenca (označený písmenom - H). Alebo cez dĺžku strán (a, b, c).

Celková plocha báz je: S = 2a * h alebo S = 2ac

Keďže bočné plochy sú obdĺžniky, ich plocha je: S = 2a * H a S = 2b * h alebo S = 2a * b, S = 2b * c

Preto sme zistili, ako nájsť túto oblasťkváder - konečný vzorec pre výpočet je zapísaná ako: S = 2AH + 2Ah + 2BH = 2 (Ah + aH + bh) alebo S = 2 (S + Z. + Sc) = 2 (ab + bc + AC), a síce, čo je dvojnásobok súčtu plôch tváre krabice.

Tam sú prípady, kedy bočné tváreRovnobežník leží pod ľubovoľným uhlom k jeho základňu, potom je rovnobežnosť sklonená. Potom sa vypočítava plocha jej bočných plôch, vediac ich výšku. V tomto prípade sa plocha základov vypočíta identicky.

Nič zložité.