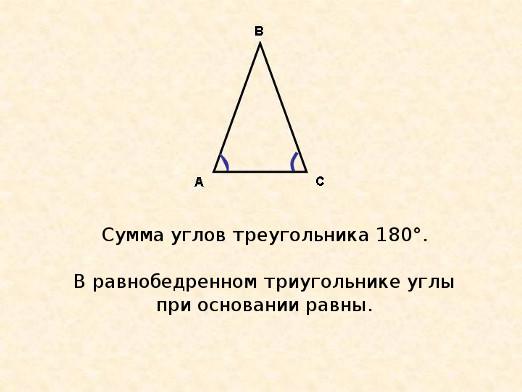
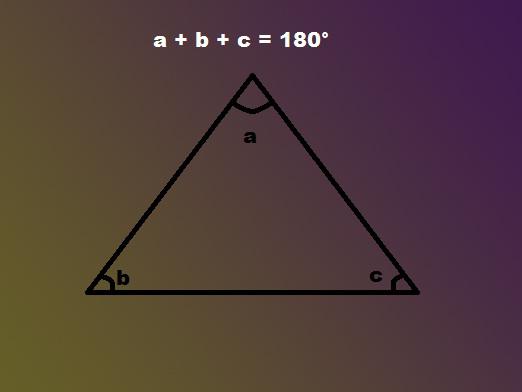
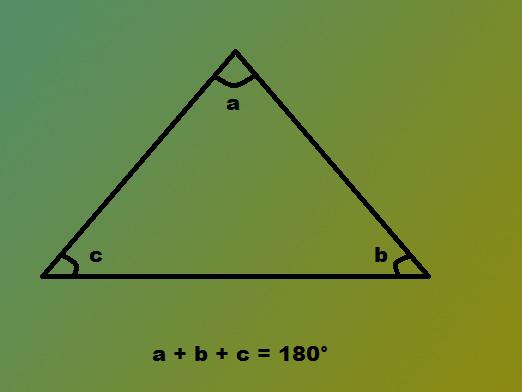
Ako nájsť uhly trojuholníka?

Pravdepodobne každý vie takú jednoduchú postavu,pozostáva z troch vzájomne prepojených línií, ako trojuholník. Zo školského programu je stále známe, ako nájsť strany trojuholníka, ale dnes si málo ľudí pamätá tie pravdivé pravidlá a vzorce. A obnoviť to v pamäti, nebolo by to vôbec neublížilo, pretože niekedy je len potrebné poznať pravidlá, ako nájsť uhly v trojuholníku, aby sa určila určitá vzdialenosť v každodennom živote.

Skúsme si spomenúť na Pythagorovu vetu,čo naznačuje, že štvorec hypotenze sa rovná súčtu štvorcov dvoch končatín. Odkazujeme na strany trojuholníka ako priečniky, ktoré sa pretínajú pod uhlom 90 stupňov. Hypotenuse je bokom medzi nimi. Keď poznáte dĺžku oboch strán, môžete vypočítať tretiu vzorec.

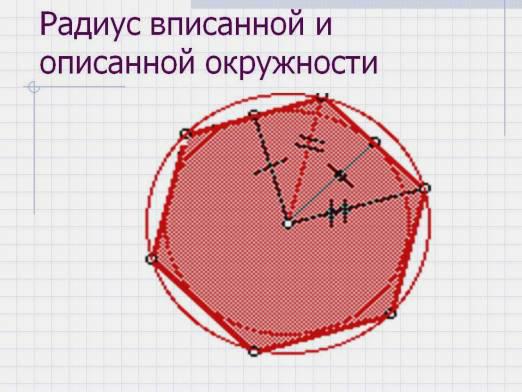
Existuje niekoľko ďalších pravidiel, ako nájsť tretiuuhol trojuholníka, ale tieto vety sú trochu komplikovanejšie. Vychádzajúc zo sínusovej vety, strany trojuholníka sú úmerné sínusom protiľahlých uhlov. To znamená, že existuje vzorec, podľa ktorého je polomer kružnice ohraničený okolo trojuholníka, vynásobený dvoma, rovný pomeru každej strany trojuholníka k sine opačného uhla. Keď poznáte údaje, môžete vypočítať chýbajúce strany. Môže sa tiež obrátiť na kosínusovú vetu, ktorá zovšeobecňuje samotnú vetu Pytagoras. Námestie jednej strany sa rovná súčtu štvorcov ostatných dvoch mínus dvojnásobný produkt týchto strán kozinusom uhla medzi nimi.

Najdôležitejšou zo všetkých týchto vzorcov je správne nahradiť údaje a nájsť neznáme, pretože nesprávne odvodenie neznámeho nedosiahne správny výsledok.