Ako nájsť oblasť postavy?

Poznať a byť schopný vypočítať rôzne oblastičísla sú potrebné nielen na riešenie jednoduchých geometrických problémov. Nerobte bez týchto znalostí a pri zostavovaní alebo kontrole odhadov na opravu priestorov, výpočet počtu požadovaných dodávok. Takže poďme zistiť, ako nájsť oblasti rôznych čísel.

rozloha

Časť roviny uzavretej v uzavretom obryse sa nazýva oblasť tejto roviny. Oblasť je vyjadrená počtom zabudovaných štvorcových jednotiek.

Na výpočet plochy základných geometrických tvarov musíte použiť správny vzorec.

Oblasť trojuholníka

Legenda:

• S je požadovaná oblasť,
• a, b, c sú dĺžky strán trojuholníka,
• h je výška požadovaného trojuholníka,
• γ je uhol medzi bočnou stranou a b,
• r je polomer kruhu (napísaný v trojuholníku),
• R je polomer kruhu (opísaný okolo trojuholníka),
• p je polovica obvodu trojuholníka.

1. Pokiaľ je známe, H, A, požadovaná plocha trojuholníka je definovaná ako súčin dĺžok trojuholníka strán a výška sa znižuje smerom k tejto strane, rozdelená na dve polovice: S = (a · h) / 2
2. Ak sú známe a, b, c, potom požadovaná oblasťvypočíta Heron vzorca: druhá odmocnina vziať produktu z polovice obvodu trojuholníka a tri rozdiely polovičné a obvodu každej strane trojuholníka: S = √ (p · (p - A) · (p - b) · (p - c)).
3. Ak sú známe a, b, γ, potom je oblasť trojuholníka definovaná ako polovica produkcie dvoch strán vynásobená hodnotou uhla sínusu medzi týmito stranami: S = (a · b · sin y) / 2
4. Ak sú známe a, b, c, R, potom je požadovaná plocha definovaná ako produkt dĺžok všetkých strán trojuholníka štyrmi polomermi ohraničenej kružnice: S = (a · b · c) / 4R
5. Ak je p, r známe, potom požadovaná plocha trojuholníka je určená vynásobením polovice obvodu polomerom kruhu, ktorý je v ňom zapísaný: S = p · r

Štvorec námestia

Legenda:

• S je požadovaná oblasť,
• a je dĺžka strany,
• d je dĺžka uhlopriečky.

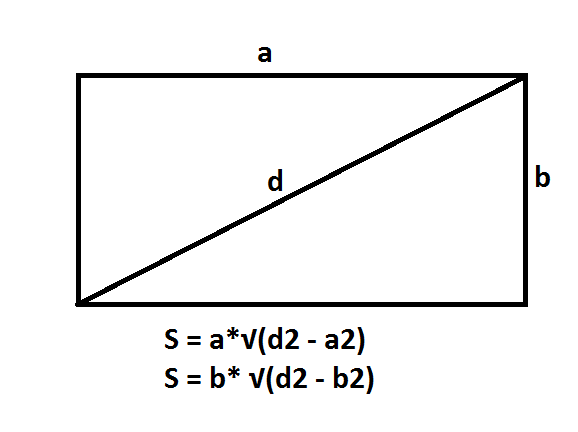
1. Ak je táto strana známa, potom je plocha tohto čísla definovaná ako štvorec dĺžky jej strany: S = a²
2. Pokiaľ je známe, d, námestie oblasť je definovaná ako polovica druhou mocninou dĺžky uhlopriečky: S = d²/ 2

Oblasť obdĺžnika

Legenda:

• S je oblasť, ktorá sa má určiť,
• a, b sú dĺžky strán obdĺžnika.

1. Ak a, b sú známe, potom je plocha tohto obdĺžnika určená produktom dĺžok jeho dvoch strán: S = a · b
2. Ak nie sú známe dĺžky strán, potom musí byť plocha obdĺžnika rozdelená na trojuholníky. V tomto prípade je oblasť obdĺžnika definovaná ako súčet oblastí jeho trojuholníkov.

Oblasť rovnobežníka

Legenda:

• S je požadovaná oblasť,
• a, b sú dĺžky bokov,
• h je dĺžka výšky tohto rovnobežníka,
• d1, d2 sú dĺžky dvoch uhlopriečok,
• α je uhol medzi stranami,
• γ je uhol medzi uhlopriečkami.

1. Ak a, h sú známe, potom je požadovaná plocha určená vynásobením dĺžok bočných strán a výškou klesnutou na tejto strane: S = a · h
2. Ak sú známe a, b, α, potom je plocha rovnobežníka určená vynásobením dĺžok strán rovnobežníka a sínusovej hodnoty uhla medzi týmito stranami: S = a · b · sin α
3. Ak poznáme d₁, d₂, Γ plocha rovnobežníka je definovaný ako polovica súčinu dĺžky uhlopriečok a sínusu uhla medzi uhlopriečok: S = (d₁· D₂· Sing) / 2

Diamond Square

Legenda:

• S je požadovaná oblasť,
• a je dĺžka strany,
• h je dĺžka výšky,
• α je menší uhol medzi oboma stranami,
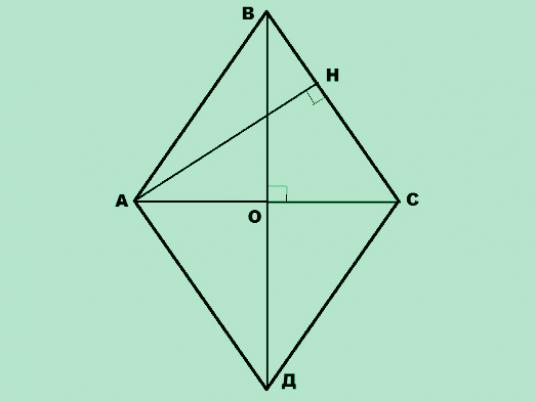
• d1, d2 sú dĺžky dvoch uhlopriečok.

1. Ak a, h sú známe, potom je oblasť kosoštvorca určená vynásobením dĺžky strany dĺžkou výšky, ktorá je znížená na túto stranu: S = a · h
2. Ak a, α sú známe, potom je kosoštvorcová oblasť určená vynásobením štvorca dĺžky strany sínusom uhla medzi stranami: S = a²Sin sin
3. Ak poznáme d₁ a d₂, potom požadovaná plocha je definovaná ako polovica produkcie dĺžok diamantov kosoštvorca: S = (d₁· D₂) / 2

Trapézna oblasť

Legenda:

• S je požadovaná oblasť,
• a, b - dĺžky 2 báz lichobežníka,
• c, d sú dĺžky ľavej a pravej strany lichobežníka,
• h je výška lichobežníka,

1. Ak sú známe a, b, c, d, požadovaná plocha je určená vzorcom: S = (a + b) / 2 * √ [c²- (((b-a)²+ c²-d²) / (2 (b-a))²].
2. Pre známe a, b, h je požadovaná plocha definovaná ako produkt polovice súčtu základov a výška lichobežníka: S = (a + b) / 2 · h

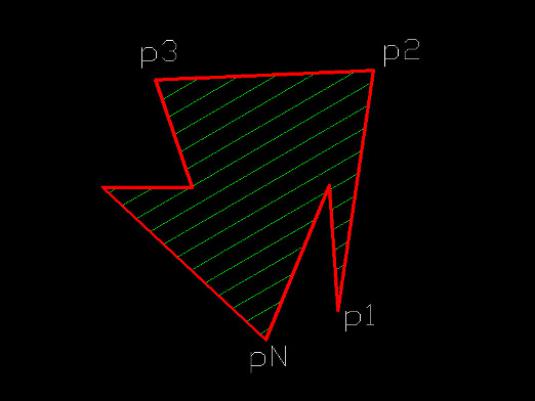
Oblasť konvexného štvoruholníka

Legenda:

• S je požadovaná oblasť,
• d₁, d₂ - dĺžky uhlopriečok daného štvoruholníka,
• α je uhol medzi uhlopriečkami,
• p = (a + b + c + d) / 2 je polovica obvodu konvexného štvoruholníka,
• a a b, c a d sú dĺžky každej strany konvexného štvoruholníka,
• θ = (α + β) / 2 je polovica súčtu dvoch protiľahlých uhlov konvexného štvoruholníka,
• r je polomer kruhu zapísaného do konvexného štvoruholníka.

1. Ak poznáme d₁, d₂, α, potom je plocha konvexného štvoruholníka definovaná ako polovica produkcie diagonálov štvoruholníka vynásobená sínusovým uhlom medzi týmito uhlopriečkami: S = (d₁· D ₂· Sin a) / 2
2. Pre známu p, r je plocha konvexného štvoruholníka definovaná ako produkt polomeru štvoruholníka polomerom kružnice zapísanej v tomto štvoruholníku: S = p · r
3. Ak sú známe a, b, c, d, θ, potom plocha konvexnéhoštvoruholník je definovaný ako druhá odmocnina rozdielu semiperimeter pracuje a dĺžka každej strany mínus produktu dĺžok všetkých strán štvorca a cos polovica súčtu dvoch protiľahlých rohoch: S² = (p - a) (p - b) (p - c) (p - d) - abcd · cos²((a + ß) / 2)

Oblasť kruhu

Legenda:

• S je požadovaná oblasť,
• r je dĺžka polomeru,
• d je dĺžka priemeru.

Ak r je známe, potom je požadovaná plocha definovaná ako produkt čísla π polomerom na štvorci: S = π r²

Ak je d známe, potom je plocha kružnice definovaná ako produkt čísla π pri štvorci priemeru, delené štyrmi: S = (π · d²) / 4

Oblasť komplexného čísla

Zložitý môže byť rozdelený na jednoduché geometrické postavy. Oblasť komplexného čísla je definovaná ako súčet alebo rozdiel v zložených oblastiach. Zvážte napríklad krúžok.

označenie:

• S je oblasť kruhu,
• R, r sú polomery vonkajšieho obvodu a vnútorné,
• D, d sú priemery vonkajšieho kruhu a vnútorný obvod.

Aby bolo možné nájsť oblasť prstenca, je potrebné zaoberať sa oblasťou

menší kruh. S = S1-S2 = pR²-πr² = π (R²-r²).

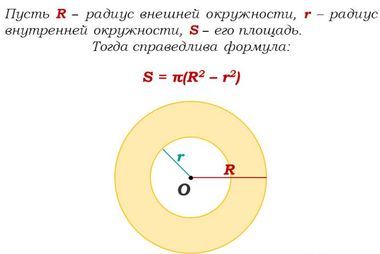
Ak teda R a r sú známe, potom je plocha prstenca definovaná ako rozdiel štvorcov polomerov vonkajšej a vnútornej kružnice vynásobený počtom pi: S = π (R²-r²).

Ak sú známe D a d, potom je plocha prstenca definovaná ako štvrtina rozdielu v štvorcoch priemerov vonkajšej a vnútornej kružnice vynásobených počtom pi: S = (1/4) (D²-d²) π.

Oblasť tieňovanej postavy

Predpokladajme, že je vnútri toho istého štvorca (A) iná (B) (menšia) a musíme nájsť tieňovú dutinu medzi obrázkami "A" a "B". Povedzme len "rám" malého štvorca. Ak to chcete urobiť:

1. Nájdeme oblasť obrázku "A" (vypočítaná podľa vzorca na nájdenie štvorca štvorca).
2. Podobne nájdeme aj oblasť obrázku "B".
3. Odpočítavame oblasť "B" z oblasti "A". A tak dostaneme oblasť stinnej postavy.

Teraz už viete nájsť oblasti rôznych tvarov.